บทที่ 13

คลื่นวัฏจักรกับค่าเฉลี่ยเคลื่อนที่

ดังที่ได้อธิบายไว้ในบทก่อนๆ เกี่ยวกับระบบค่าเฉลี่ยเคลื่อนแล้ว คงจะยังพอจำกันได้นะครับ ว่า moving average นั้น เป็นการกรองเอาความผิดปกติ (noise) ออกจากข้อมูลแบบหนึ่ง อันที่จริงแล้ว ในทางสถิติ เราถือว่า moving average เป็น Low-Pass Filter แบบหนึ่ง ที่เรียกว่าเป็น Low-Pass Filter เพราะว่าถ้าเราเอาข้อมูลมาทำค่าเฉลี่ยเคลื่อนที่ สมมติว่า 100 วัน เราจะพบว่า วัฏจักรที่มีความยาวคลื่นน้อยกว่า 100 วัน จะถูกกรองทิ้งออกไป อันเป็นผลเนื่องมาจากการคำนวณค่าเฉลี่ย ตัวอย่างเช่น ถ้าเรามีข้อมูลรายเดือน ซึ่งมีผลของฤดูกาล (สมมติว่าเป็นราคาทุเรียนแล้วกันครับ เห็นชัดดี) มาเฉลี่ยแบบเคลื่อนที่ 12 เดือน เราก็จะพบว่าตัวเลขค่าเฉลี่ยเคลื่อนที่ 12 เดือนนี้ ไม่มีผลของฤดูกาลหลงเหลืออยู่ เพราะว่ามันเฉลี่ยกันไปทั้งปีหมดไปแล้ว

สิ่งที่ยังคงหลงเหลืออยู่ใน moving average คือ คลื่นวัฏจักรที่มีความยาวคลื่นมากกว่าค่าเฉลี่ยเคลื่อนที่ คงจะยังไม่ลืมนะครับว่า คลื่นที่มีความยาวคลื่นมาก จะมีความถี่ต่ำ ดังนั้น เราพูดอีกอย่างหนึ่งได้ว่า สิ่งที่ moving average ไม่ได้กรองทิ้งไป ก็คือ คลื่นที่มีความถี่ต่ำกว่านั่นเอง และนี่เป็นที่มาของคำว่า Low-Pass Filter ครับ

ถ้าจะพูดกันอย่างเคร่งครัดจริงๆ moving average ก็ไม่ได้กรองคลื่นที่มีความยาวคลื่นน้อยกว่าค่าเฉลี่ยเคลื่อนที่ออกไปได้ทั้งหมดหรอกครับ ยกตัวอย่างสักหน่อยแล้วกันนะครับ สมมติว่าเราคำนวณค่าเฉลี่ยเคลื่อนที่ 100 วัน ในข้อมูลที่มีวัฏจักรที่มีความยาวคลื่น 70 วันอยู่ด้วย เราจะพบว่า ในรอบ 100 วันที่เราทำการเฉลี่ย จะมีรอบวัฏจักรขนาด 70 วันอยู่ด้วย 1 รอบ กับอีก 30 วัน (เกือบรอบครึ่ง) แน่นอนครับไอ้ที่ครบรอบนั่นมันหักล้างกันหมดไปแน่ละ แต่ไอ้เจ้า 30 วันที่เหลือ (ซึ่งอาจจะอยู่ที่หัวบ้าง ท้ายบ้าง แล้วแต่ Phase ของวัฏจักร 70 วัน) นี่มันคงจะไม่ได้หักล้างกันหมดไปซะทีเดียว อย่างไรก็ดีผลของวัฏจักร 70 วันนี้ ก็ถูกกรองออกไปเยอะพอสมควรแล้ว การกรองสัญญาณจะสามารถกรองได้หมด ก็ต่อเมื่อระยะเวลาที่ใช้ในการคำนวณค่าเฉลี่ยเคลื่อนที่ มีค่าเป็นจำนวนเท่า (multiple) ของคลื่นวัฏจักรเท่านั้น ตัวอย่างเช่น ถ้าคำนวณค่าเฉลี่ยเคลื่อนที่ 100 วัน ในข้อมูลที่มีวัฏจักรขนาด 50 วัน การเฉลี่ยเคลื่อนที่จะตัดผลของวัฏจักร 50 วันออกไปได้หมดจดทีเดียว (เพราะเฉลี่ย 100 วัน มันเฉลี่ย 50 วัน ไป 2 รอบ ซึ่งผลก็ยังหักล้างกันอยู่ดี)

ทีนี้ เราจะลองเอา moving average มาทำอะไรกับข้อมูลราคาที่เราสนใจได้บ้าง สมมติว่าเรารู้แล้วว่าข้อมูลราคานั้นประกอบด้วยวัฏจักรที่มีระยะเวลา 100 วัน ถ้าเราคำนวณ moving average ระยะเวลา 100 วันเท่ากับความยาวคลื่นของวัฏจักร ผลที่ได้เหรอครับ ก็โบ๋เบ๋ไงครับ เพราะวัฏจักรมันหักล้างกันหมดไปพอดี อันที่จริงถ้าข้อมูลประกอบด้วยวัฏจักรขนาด 100 วันเพียงอย่างเดียว สิ่งที่คุณจะได้จากค่าเฉลี่ยเคลื่อนที่ก็คือ ค่าเฉลี่ยของ 1 รอบวัฏจักร แล้วก็มีค่าคงที่แบบนั้นตลอดไป แต่ถ้าข้อมูลประกอบด้วยคลื่นวัฏจักรขนาด 100 วันกับวัฏจักรขนาด 200 วัน สิ่งที่คุณได้จาก 100 - day moving average ก็คือคลื่นวัฏจักรขนาด 200 วัน สรุปแล้วก็คือการทำ moving average ที่มีระยะเวลาเท่ากับรอบวัฏจักร คงจะไม่ให้ผลอะไรแก่เรามากนัก

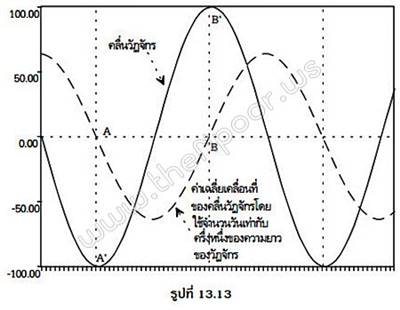
ที่น่าสนใจหน่อยคือการทำ moving average ที่มีระยะเวลาเท่ากับครึ่งรอบวัฏจักร สมมติว่าวัฏจักรในข้อมูลเรา เป็นวัฏจักรขนาด 50 วันฉบับแท้และดั้งเดิม กล่าวคือมีความสมมาตรและสม่ำเสมอ ดังแสดงในรูปที่ 13.13 ถ้าเราคำนวณค่าเฉลี่ยเคลื่อนที่ขนาด 25 วัน (ครึ่งหนึ่งของรอบวัฏจักร) เราจะพบว่า ค่าเฉลี่ยเคลื่อนที่นี้ จะวิ่งจากค่าบวกมาเป็น 0 เมื่อวัฏจักรกำลังพลิกตัวที่จุดต่ำสุดพอดี (จุด A และ A’ ในรูปที่ 13.13) ดังนั้น ถ้าหากค่าเฉลี่ยเคลื่อนที่วิ่งจากลบเข้าหา 0 แสดงว่าราคาใกล้ที่จะถึงจุดยอดเต็มที และถ้าค่าเฉลี่ยเคลื่อนที่วิ่งจากบวกเข้าหา 0 แสดงว่าราคาใกล้จะถึงจุดต่ำสุดมากแล้วครับ

ปรากฏการณ์นี้ เราสามารถพูดได้อีกอย่างหนึ่งว่า moving average ขนาดครึ่งรอบวัฎจักร มี Phase-Lag เท่ากับ 90 องศาพอดี เมื่อเทียบกับตัววัฏจักร ทั้งนี้เพราะกว่าค่า moving average จะวิ่งเข้าหาจุด 0 ก็เป็นเวลาที่ phase Angle ของวัฏจักรเท่ากับ 90 องศาพอดี (ถ้างง ลองย้อนกลับไปอ่านเรื่องการวัด phase Angle อีกทีนะครับ)

ทีนี้ในโลกของความเป็นจริง ข้อมูลมันไม่ได้ประกอบด้วยวัฏจักรเดียว แต่อาจจะประกอบด้วยวัฎจักรจำนวนมาก ดังนั้น เราก็ต้องปรับปรุงสูตรของเราให้มันเข้ากับความเป็นจริงมากขึ้น วิธีการก็คือ คำนวณค่าเฉลี่ยเคลื่อนที่ 2 อัน อันแรกมีระยะเวลาเท่ากับครึ่งหนึ่งของความยาววัฎจักร (เรียกว่า MA-Half แล้วกันนะครับ สั้นหน่อย) อันที่สองมีระยะเวลาเท่ากับความยาววัฏจักรพอดี (เรียกย่อๆว่า MA-Full) ในกรณีที่ข้อมูลประกอบด้วยหลายๆวัฏจักร การคำนวณค่าเฉลี่ยเคลื่อนที่โดยใช้ระยะเวลาเท่ากับความยาววัฏจักรจะไม่ได้เส้นตรงที่ราบเรียบ แต่สิ่งที่ได้คือแนวโน้มหรือวัฏจักรอื่นๆที่มีความยาวคลื่นมากกว่าอันที่เรากำลังตามอยู่ ส่วนวัฎจักรที่มีความยาวคลื่นน้อยกว่าก็จะถูกกรองออกไป

ทีนี้เราก็ใช้สูตรเดิมครับ คือ ถ้า MA-Half ตัด MA-Full จากข้างบนลงข้างล่างจะเป็นสัญญาณซื้อ และถ้า MA-Half ตัด MA-Full จากข้างล่างขึ้นข้างบน เป็นสัญญาณขาย จะเห็นว่าการให้สัญญาณจะตรงกันข้ามกับสัญญาณของ double moving average นะครับ กล่าวคือ แทนที่ตัดขึ้นจะซื้อ กลับขาย และแทนที่ตัดลงจะขาย กลับซื้อ

เนื้อหาต่อไป : วัฏจักรกับ Momentum

เนื้อหาก่อนหน้า : การใช้วัฏจักรกับเครื่องมือการวิเคราะห์ทางเทคนิคอื่นๆ